10 PID

When you design a rolling robot with 2 motors (the classic differential steering configuration), one of the very first problem is to go on a straight-line path. Even a small difference between the 2 motors introduce an important deviation, so it's necessary to use a regulation process. PID regulation is a well known algorithm that takes in account Proportional, Integral and Derivative control.

There is lot of information about PID regulation and robots, for example, there are very precise details about the ways to tune the 3 ponderations (KI, KP, KD) in thousands of web pages, but, very often there is no information about a basic implementation choice: the clear definition of the system. In fact, all you need to start is in this article ``Using a PID-based Technique For Competitive Odometry and Dead-Reckoning''
http://www.seattlerobotics.org/encoder/200108/using_a_pid.html
but, you may miss the the key point (as I did first), which is, you have to clearly choose the global regulation strategy. There are several ways to view this regulation system:

2 independent regulations (one for each motor)
2 independent regulations, PLUS a global regulation (to control the real position of the robot)
2 shared but independent regulations: one for the speed, and one for the orientation
only one regulation on the orientation (because the actual speed is not very important).

Lots of people don't clearly say the type of regulation strategy they used, and it seems that beginners often use the first strategy because it's the simplest (tough probably the least effective). As it was said in ``Using a PID-based Technique For Competitive Odometry and Dead-Reckoning'', the last option (a single regulation on orientation), is a reasonable solution (simple and efficient).
Let's explore this solution: we consider that there is only one global system (the Robot), and not 2 (on for each motor). We start with a common command on the 2 motors (Cini=50%), and we make a regulation on the shift between these the right command (Cr) and left command (Cl) (Figure 17.1).

**Figure 17.1:** PID strategy, one regulation on the shift between Right and Left command (Cr and Cl) by using the 3 terms: Proportional (lateral velocity Vy), Integral (lateral error Y) and Derivative (lateral acceleration Ay)
$\begin{figure}\centering\epsfig{file=graphics/pid_strategy.eps, height=4cm}\end{figure}$

So, now that we have defined the regulation strategy, we go back to a more classical discussion about the importance of the 3 regulation terms (Proportional, Integration, and Derivative) with some simulations. On all these simulations, differences between the motors are the same, and ponderations between terms (when they exist) are the same.

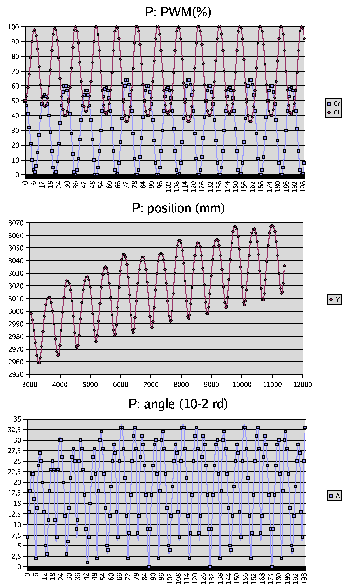
First, with only P regulation: on figure 17.2, you see that there is no real convergence of the system. There is a kind of over-correction due to a lack of anticipation, so the system stay in oscillation.

**Figure 17.2:** P regulation
$\begin{figure}\centering\epsfig{file=graphics/p.eps, height=15cm}\end{figure}$

Then, with P and D regulation: on figure 17.3, there is a convergence in the end, but the system keep a bias, because it has no idea about the effect of error accumulation before the convergence: it's a lack of memory.

**Figure 17.3:** PD regulation
$\begin{figure}\centering\epsfig{file=graphics/pd.eps, height=15cm}\end{figure}$

And, finally, with a complete PID regulation (see figure 17.4), there is no oscillations, and no bias.

**Figure 17.4:** PID regulation
$\begin{figure}\centering\epsfig{file=graphics/pid.eps, height=15cm}\end{figure}$

These simulations have been done with this program: http://botzilla.free.fr/pid/pid_simul.tgz.

botzilla@free.fr , http://botzilla.free.fr/